
下列正确的是( )

A.
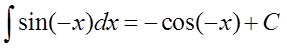

B.
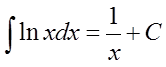

C.
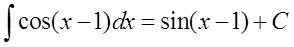

D.
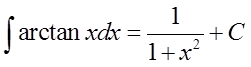
若 f(x)在 [a,b]上连续,则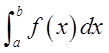 一定存在.
一定存在.
 A.
A. B.
B.设曲线 y=2x-2x3+x4,则在区间(1,2)和 (2,4)内,曲线分别为( )

A.
凹的、凸的

B.
凸的、凹的

C.
凸的、凸的

D.
凹的、凹的
函数商的导数等于函数导数的商.
 A.
A. B.
B.函数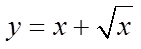 在区间[0,4]上的最小值为 ( )
在区间[0,4]上的最小值为 ( )

A.
1

B.
4

C.
3

D.
0
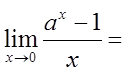 ( )
( )

A.
∞

B.
a

C.
lna

D.
1
当 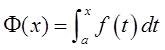 时,
时, 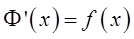 .
.
 A.
A. B.
B.若函数y=f(x)在点x0处的导数f'(x0)<0,则曲线在该点处的切线的倾斜角是( )

A.
90o

B.
钝角

C.
0o

D.
锐角
设函数f(x)在区间(a,b) 内满足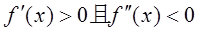 ,则函数在此区间内是( )
,则函数在此区间内是( )

A.
单调减少且是凸的

B.
单调增加且是凹的

C.
单调减少且是凹的

D.
单调增加且是凸的
已知f(x)=arcsinx,则f(-1)=( )

A.


B.


C.


D.

广义积分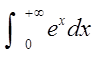 是发散的.
是发散的.
 A.
A. B.
B.设y=xe-x ,则y''=( )

A.
e-x(2-x)

B.
e-x(x+2)

C.
e-x(x-2)

D.
x2e-x
函数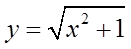 的复合过程是
的复合过程是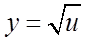 ,
,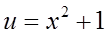 .
.
 A.
A. B.
B.下列等式正确的是( )

A.
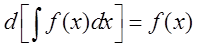

B.
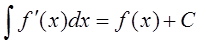

C.
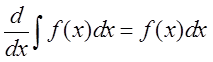

D.
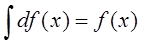
函数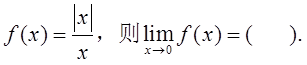

A.
-1

B.
0

C.
不存在

D.
1
若函数f(x)在x=1处可导,且f'(1)=2,则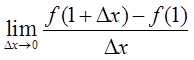 的值为( )
的值为( )

A.
0

B.
3

C.
2

D.
1
设函数f(x)在区间(a,b)内满足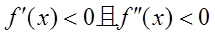 ,则函数在此区间内是( )
,则函数在此区间内是( )

A.
单调增加且是凸的

B.
单调减少且是凹的

C.
单调减少且是凸的

D.
单调增加且是凹的
极值点必是拐点.
 A.
A. B.
B.初等函数在定义域区间内都是连续的.
 A.
A. B.
B.函数积的导数等于函数导数的积.
 A.
A. B.
B.设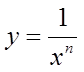 ,则y'=( )
,则y'=( )

A.
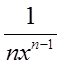

B.
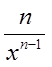

C.
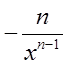

D.
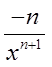
极限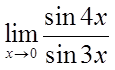 的值为( )
的值为( )

A.
-1

B.
1

C.
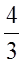

D.
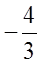
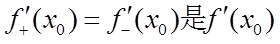 存在的( )条件
存在的( )条件

A.
无关系

B.
充分非必要

C.
充分必要

D.
必要
函数商的导数等于函数导数的商.
 A.
A. B.
B.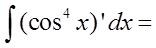 ( )
( )

A.
sinxcos3x+C

B.
sin3xcosx+C

C.
sin2xcos2x+C

D.
cos4x+C
函数y=2x2的拐点为( )

A.
不存在

B.
(1,0)

C.
(1,1)

D.
(0,0)
在区间(0,1)内为减函数的是( )

A.
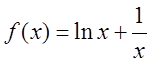

B.
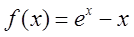

C.
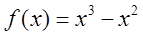

D.
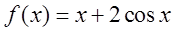
定积分是变量x的函数.
 A.
A. B.
B.连续函数一定有界.
 A.
A. B.
B.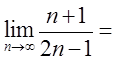 ( )
( )

A.
∞

B.
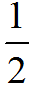

C.
2

D.
1
若函数f(x) 在x0 点不连续,则f(x0)必不存在.
 A.
A. B.
B.函数y=3-x2有极小值3.
 A.
A. B.
B.函数 y=|x|的连续区间是( )

A.
(0,+∞)

B.
(-∞,+∞)

C.
[-1,1]

D.
(-∞,0)
函数在某点不可导,函数所表示的曲线在相应点的切线( )

A.
一定不存在

B.
不一定不存在

C.
一定平行于y 轴

D.
一定存在
如果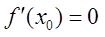 ,则x=x0为f(x)的极值.
,则x=x0为f(x)的极值.
 A.
A. B.
B.y=arcsinu,u=2+x的复合函数是y=arcsin(2+x) .
 A.
A. B.
B.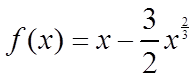 的极值点的个数是( )
的极值点的个数是( )

A.
3个

B.
1个

C.
0个

D.
2个
函数y=f(x)在x0可导,则在x0处的切线存在.
 A.
A. B.
B.函数的增量就是该函数的微分.
 A.
A. B.
B.函数y=2x3-9x2+12x-9的单调减少区间是( )

A.
(2,3)

B.
(-1,2)

C.
(1,2)

D.
(1,3)
设函数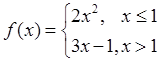 ,则函数f(x)在点x=1 处( )
,则函数f(x)在点x=1 处( )

A.
可导

B.
不连续

C.
连续但不可导

D.
连续但左、右导数不存在
若f'(x)=g'(x),则f(x)=g(x).
 A.
A. B.
B.若 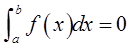 则f(x)=0 .
则f(x)=0 .
 A.
A. B.
B.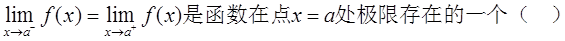

A.
必要条件

B.
无关条件

C.
充要条件

D.
充分条件
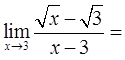 ( )
( )

A.
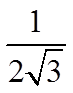

B.
3

C.
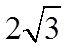

D.
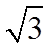
已知 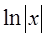 是f(x)的一个原函数,则下列式子中也是f(x)的原函数的是( )
是f(x)的一个原函数,则下列式子中也是f(x)的原函数的是( )

A.
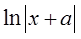

B.
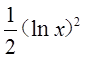

C.
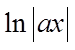

D.
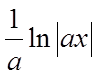
若e-x是f(x)的一个原函数,则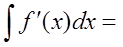 ( )
( )

A.
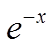

B.
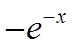

C.
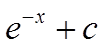

D.
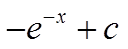
函数y=f(x)在x0处可导,则在x0处的切线存在.
 A.
A. B.
B.y=sin2xcos2x 是奇函数.
 A.
A. B.
B.y=xlnx的二阶导数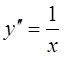 .
.
 A.
A. B.
B.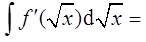 ( )
( )

A.
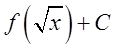

B.
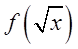

C.
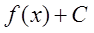

D.
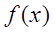
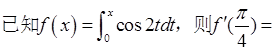 ( )
( )

A.
2

B.
0

C.
-1

D.
1
函数的最大值是函数的最值.
 A.
A. B.
B.已知y=sinx ,则 y(10)= ( )

A.
-cosx

B.
-sinx

C.
sinx

D.
cosx
设函数 ,如果函数在
,如果函数在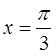 处取得极值,则a=( )
处取得极值,则a=( )

A.
3

B.
1

C.
2

D.
0
曲线x2=6y-y3在(-2,2)点的切线的斜率为( )

A.
-1

B.
2

C.
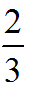

D.
0
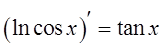
 A.
A. B.
B.函数f(x)的原函数加上常数就是不定积分.
 A.
A. B.
B.如果曲线y=f(x)在点x0不可导,则曲线在点(x0,f(x0)) 处切线不存在.
 A.
A. B.
B.若函数f(x)在x=1处可导,且f'(1)=2则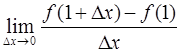 的值为( )
的值为( )

A.
1

B.
2

C.
0

D.
3